Page 126 - ДисМокрий21

126

між променями, що інтерферують. Цікавим є випадок, коли ширина

інтерференційних ліній є співмірною з довжиною ПАХ. Для аналізу такої

ситуації необхідно повернутись до розгляду виразу (2.20). Він дозволяє знайти

умови, за яких чутливість інтерферометра Майкельсона не буде залежати від

зміни різниці ходу d і, відповідно, буде стабільною. З вигляду виразу (2.20)

можна зробити висновок, що d не буде впливати на чутливість, коли один з

доданків дорівнюватиме ну-
I ≈,в.о.
лю. В цьому випадку інший
1 доданок буде визначати вели-

чину сигналу з фотоприймача.

Зміна різниці ходу приз-

2 водитиме лише до зміни фази

сигналу, але амплітуда сигналу
не буде змінюватись. Таким
r, мм
чином, можна назвати дві
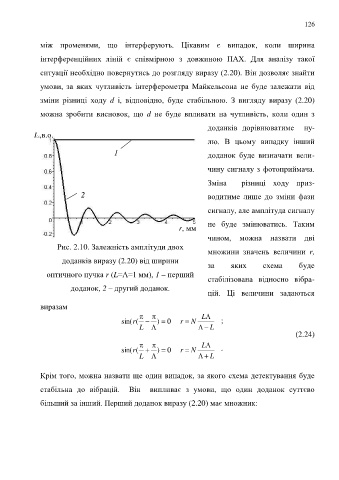
Рис. 2.10. Залежність амплітуди двох
множини значень величини r,
доданків виразу (2.20) від ширини
за яких схема буде
оптичного пучка r (L=Λ=1 мм), 1 – перший
стабілізована відносно вібра-
доданок, 2 – другий доданок.
цій. Ці величини задаються

виразам
  L
sin(r (  )  0 r  N ;
L    L
(2.24)
  L
sin(r (  )  0 r  N .
L    L

Крім того, можна назвати ще один випадок, за якого схема детектування буде

стабільна до вібрацій. Він випливає з умови, що один доданок суттєво

більший за інший. Перший доданок виразу (2.20) має множник: