Page 87 - РОЗДІЛ 1

87

ймовірності  = 0,95 і кількості степенів свободи k = 16 – 2 за таблицею [265]

знаходимо критичне значення статистики критерію  2 = 23.7. Так як критичне
0,05
значення виявилось більшим (23,7 > 15,8), ніж обчислене за статистичними дани-

ми, то гіпотезу про належність вибірки експоненційному розподілу необхідно

прийняти.

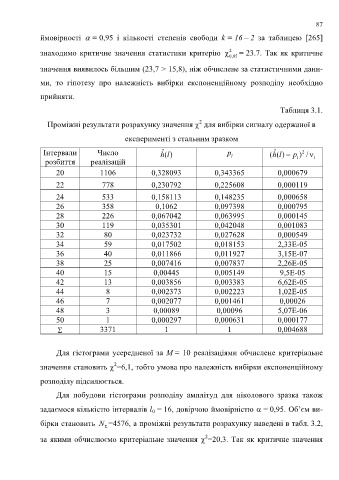
Таблиця 3.1.

2
Проміжні результати розрахунку значення  для вибірки сигналу одержаної в
експерименті з стальним зразком

ˆ
ˆ
Інтервали Число hl p (( )  p ) /
2
()
hl
l
розбиття реалізацій l l
20 1106 0,328093 0,343365 0,000679
22 778 0,230792 0,225608 0,000119
24 533 0,158113 0,148235 0,000658
26 358 0,1062 0,097398 0,000795
28 226 0,067042 0,063995 0,000145
30 119 0,035301 0,042048 0,001083
32 80 0,023732 0,027628 0,000549
34 59 0,017502 0,018153 2,33E-05

36 40 0,011866 0,011927 3,15E-07
38 25 0,007416 0,007837 2,26E-05
40 15 0,00445 0,005149 9,5E-05
42 13 0,003856 0,003383 6,62E-05
44 8 0,002373 0,002223 1,02E-05
46 7 0,002077 0,001461 0,00026
48 3 0,00089 0,00096 5,07E-06
50 1 0,000297 0,000631 0,000177
 3371 1 1 0,004688

Для гістограми усередненої за M = 10 реалізаціями обчислене критеріальне

2
значення становить  =6,1, тобто умова про належність вибірки експоненційному

розподілу підсилюється.

Для побудови гістограми розподілу амплітуд для ніколового зразка також

задаємося кількістю інтервалів l 0 = 16, довірчою ймовірністю  = 0,95. Об’єм ви-

бірки становить N =4576, а проміжні результати розрахунку наведені в табл. 3.2,

2
за якими обчислюємо критеріальне значення  =20,3. Так як критичне значення