Page 138 - Microsoft Word - Дисертація.docx

138

  x − x 2 
2
  1 − i  , якщо x − x < h
k h ( − xx i )= π  h 2  i .
  
 у , 0 всіх решта випадках

Широко застосовується апроксимація у вигляді функції ядра на

основі Гаусового розподілу:

2
x −x i
1 − 2
k h ( − xx i ) = e 2σ ,
2πσ 2

де σ - це середньоквадратичне відхилення розподілу, яке відіграє роль

масштабного параметра h функції Єпанечнікова. На рис.3.7 наведено

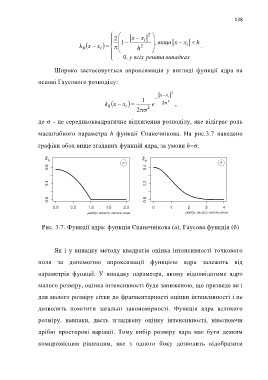
графіки обох вище згаданих функцій ядра, за умови h=σ.

Рис. 3.7. Функції ядра: функція Єпанечнікова (а), Гаусова функція (б)

Як і у випадку методу квадратів оцінка інтенсивності точкового

поля за допомогою апроксимації функцією ядра залежить від

параметрів функції. У випадку параметра, якому відповідатиме ядро

малого розміру, оцінка інтенсивності буде заниженою, що призведе як і

для малого розміру сітки до фрагментарності оцінки інтенсивності і не

дозволить помітити загальні закономірності. Функція ядра великого

розміру, навпаки, дасть згладжену оцінку інтенсивності, нівелюючи

дрібні просторові варіації. Тому вибір розміру ядра має бути деяким

компромісним рішенням, яке з одного боку дозволить відобразити