Page 119 - disertation_SLIEPKO_ROMAN
P. 119
119
2 2 2
F f 0 1 6.17 2 m c , F f 0 2 6.49 2 m c , F f 0 3 5.91 2 m c . Ці величини
1
1
1
визначають сумарну потужність десяти гармонічних складових математичного
сподівання, що описує детерміновану складову вібрацій. Як бачимо, потужність
детермінованих коливань для різних стадій відрізняється незначно.
Підставивши до формули (4.3) замість f відповідні значення базових
частот f 0 i , i 1,3, обчислимо коефіцієнти Фурʼє математичного сподівання
ˆ
ˆ
i
i
ˆ m k c і ˆ m k s , а також амплітуди гармонік
f
f
0
0
ˆA kf c k 2 m k s 2 . (4.4).
ˆ
ˆ
ˆ
i
i
i
f
ˆ m
f
0
0
0
а) б)
в)
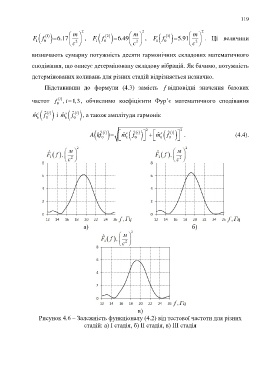
Рисунок 4.6 – Залежність функціоналу (4.2) від тестової частоти для різних
стадій: а) І стадія, б) ІІ стадія, в) ІІІ стадія
2 2 2
F f 0 1 6.17 2 m c , F f 0 2 6.49 2 m c , F f 0 3 5.91 2 m c . Ці величини
1
1
1
визначають сумарну потужність десяти гармонічних складових математичного
сподівання, що описує детерміновану складову вібрацій. Як бачимо, потужність
детермінованих коливань для різних стадій відрізняється незначно.
Підставивши до формули (4.3) замість f відповідні значення базових
частот f 0 i , i 1,3, обчислимо коефіцієнти Фурʼє математичного сподівання
ˆ
ˆ
i
i
ˆ m k c і ˆ m k s , а також амплітуди гармонік
f
f
0
0
ˆA kf c k 2 m k s 2 . (4.4).
ˆ
ˆ
ˆ
i
i
i
f
ˆ m
f
0
0
0
а) б)
в)
Рисунок 4.6 – Залежність функціоналу (4.2) від тестової частоти для різних
стадій: а) І стадія, б) ІІ стадія, в) ІІІ стадія