Page 121 - disertation_SLIEPKO_ROMAN

121

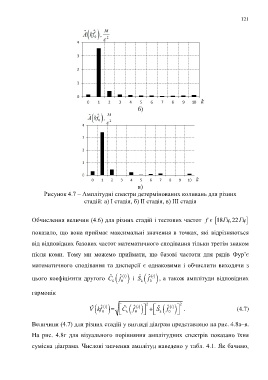
б)

в)
Рисунок 4.7 – Амплітудні спектри детермінованих коливань для різних
стадій: а) І стадія, б) ІІ стадія, в) ІІІ стадія



Обчислення величин (4.6) для різних стадій і тестових частот f є 18Гц ,22Гц
показало, що вона приймає максимальні значення в точках, які відрізняються

від відповідних базових частот математичного сподівання тільки третім знаком

після коми. Тому ми можемо приймати, що базові частоти для рядів Фурʼє

математичного сподівання та дисперсії є однаковими і обчислити виходячи з

ˆ
ˆ
  i
  i
f
f
цього коефіцієнти другого С ˆ k   і S ˆ k   , а також амплітуди відповідних
0
0
гармонік
 
ˆ
ˆ
ˆ
ˆˆ
  i
  i
f
V kf ˆ 0   i   С k    2   S k    2 . (4.7)
f
0
0
   
Величини (4.7) для різних стадій у вигляді діаграм представлено на рис. 4.8a–в.
На рис. 4.8г для візуального порівняння амплітудних спектрів показано їхня
сумісна діаграма. Числові значення амплітуд наведено у табл. 4.1. Як бачимо,