Page 102 - disertation_SLIEPKO_ROMAN
P. 102
102
б)
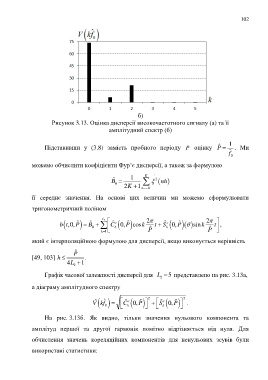
Рисунок 3.13. Оцінка дисперсії високочастотного сигналу (а) та її
амплітудний спектр (б)
ˆ
Підставивши у (3.8) замість пробного періоду P оцінку P 1 . Ми
f ˆ 0
можемо обчислити коефіцієнти Фур’є дисперсії, а також за формулою
K
ˆ
nh
B 0 1 2
2K 1 n K
її середнє значення. На основі цих величин ми можемо сформулювати
тригонометричний поліном
1 L
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
0,P
0,P
b t ,0,P B 0 C k c cosk 2 t S k c sin k 2 t ,
ˆ
ˆ
k 1 P P
який є інтерполяційною формулою для дисперсії, якщо виконується нерівність
ˆ
P
[49, 103] h .
4L 2 1
Графік часової залежності дисперсії для L 2 5 представлено на рис. 3.13а,
а діаграму амплітудного спектру
ˆ
ˆ
ˆ
ˆ
ˆ
V kf ˆ 0 C k c 2 S k c 2 .
0,P
0,P
На рис. 3.13б. Як видно, тільки значення нульового компонента та
амплітуд першої та другої гармонік помітно відрізняється від нуля. Для
обчислення значень кореляційних компонентів для ненульових зсувів були
використані статистики:
б)
Рисунок 3.13. Оцінка дисперсії високочастотного сигналу (а) та її
амплітудний спектр (б)
ˆ
Підставивши у (3.8) замість пробного періоду P оцінку P 1 . Ми
f ˆ 0
можемо обчислити коефіцієнти Фур’є дисперсії, а також за формулою
K
ˆ
nh
B 0 1 2
2K 1 n K
її середнє значення. На основі цих величин ми можемо сформулювати
тригонометричний поліном
1 L
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
0,P
0,P
b t ,0,P B 0 C k c cosk 2 t S k c sin k 2 t ,
ˆ
ˆ
k 1 P P
який є інтерполяційною формулою для дисперсії, якщо виконується нерівність
ˆ
P
[49, 103] h .
4L 2 1
Графік часової залежності дисперсії для L 2 5 представлено на рис. 3.13а,
а діаграму амплітудного спектру
ˆ
ˆ
ˆ
ˆ
ˆ
V kf ˆ 0 C k c 2 S k c 2 .
0,P
0,P
На рис. 3.13б. Як видно, тільки значення нульового компонента та
амплітуд першої та другої гармонік помітно відрізняється від нуля. Для
обчислення значень кореляційних компонентів для ненульових зсувів були
використані статистики: