Page 101 - disertation_SLIEPKO_ROMAN
P. 101
101
2 L
ˆ
ˆ
ˆ
R nh , R k c cos k 2 nh R k s sin k 2 nh ,
k 1
2
ˆ k c 2 2 nh cosk nh , (3.8)
R
K
ˆ
R k s 2 K 1 n K sink 2 nh
і L є числом вибраних для аналізу гармонік дисперсії. На рис.3.12
2
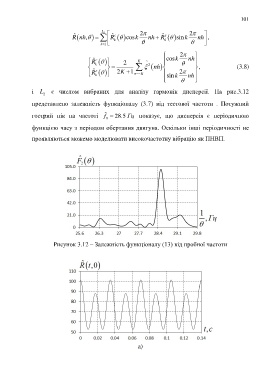
представлено залежність функціоналу (3.7) від тестової частоти . Потужний
гострий пік на частоті f ˆ 0 2 8.5 Гц показує, що дисперсія є періодичною
функцією часу з періодом обертання двигуна. Оскільки інші періодичності не
проявляються можемо моделювати високочастотну вібрацію як ПНВП.
Рисунок 3.12 – Залежність функціоналу (13) від пробної частоти
a)
2 L
ˆ
ˆ
ˆ
R nh , R k c cos k 2 nh R k s sin k 2 nh ,
k 1
2
ˆ k c 2 2 nh cosk nh , (3.8)
R
K
ˆ
R k s 2 K 1 n K sink 2 nh
і L є числом вибраних для аналізу гармонік дисперсії. На рис.3.12
2
представлено залежність функціоналу (3.7) від тестової частоти . Потужний
гострий пік на частоті f ˆ 0 2 8.5 Гц показує, що дисперсія є періодичною
функцією часу з періодом обертання двигуна. Оскільки інші періодичності не
проявляються можемо моделювати високочастотну вібрацію як ПНВП.
Рисунок 3.12 – Залежність функціоналу (13) від пробної частоти
a)