Page 100 - disertation_SLIEPKO_ROMAN
P. 100
100
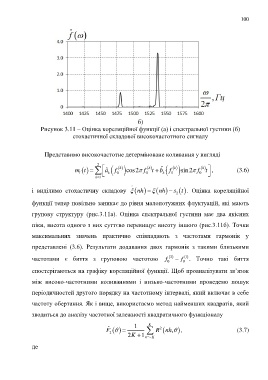
б)
Рисунок 3.11 – Оцінка кореляційної функції (а) і спектральної густини (б)
стохастичної складової високочастотного сигналу
Представимо високочастотне детерміноване коливання у вигляді
2
k
k
k
f
m 1 ˆ a k cos2 t 0 k ˆ k sin2 f t b f f t , (3.6)
0
0
0
k 1
і виділимо стохастичну складову nh nh s 2 t . Оцінка кореляційної
функції тепер повільно заникає до рівня малопотужних флуктуацій, які мають
групову структуру (рис.3.11а). Оцінка спектральної густини має два якісних
піки, висота одного з них суттєво перевищує висоту іншого (рис.3.11б). Точки
максимальних значень практично співпадають з частотами гармонік у
представлені (3.6). Результати додавання двох гармонік з такими близькими
частотами є биття з груповою частотою f 0 2 f 0 1 . Точно такі биття
спостерігаються на графіку кореляційної функції. Щоб проаналізувати зв’язок
між високо-частотними коливаннями і низько-частотними проведемо пошук
періодичностей другого порядку на частотному інтервалі, який включає в себе
частоту обертання. Як і вище, використаємо метод найменших квадратів, який
зводиться до аналізу частотної залежності квадратичного функціоналу
K
ˆ
F 2 1 R 2 nh , , (3.7)
2 K 1 n K
де
б)
Рисунок 3.11 – Оцінка кореляційної функції (а) і спектральної густини (б)
стохастичної складової високочастотного сигналу
Представимо високочастотне детерміноване коливання у вигляді
2
k
k
k
f
m 1 ˆ a k cos2 t 0 k ˆ k sin2 f t b f f t , (3.6)
0
0
0
k 1
і виділимо стохастичну складову nh nh s 2 t . Оцінка кореляційної
функції тепер повільно заникає до рівня малопотужних флуктуацій, які мають
групову структуру (рис.3.11а). Оцінка спектральної густини має два якісних
піки, висота одного з них суттєво перевищує висоту іншого (рис.3.11б). Точки
максимальних значень практично співпадають з частотами гармонік у
представлені (3.6). Результати додавання двох гармонік з такими близькими
частотами є биття з груповою частотою f 0 2 f 0 1 . Точно такі биття
спостерігаються на графіку кореляційної функції. Щоб проаналізувати зв’язок
між високо-частотними коливаннями і низько-частотними проведемо пошук
періодичностей другого порядку на частотному інтервалі, який включає в себе
частоту обертання. Як і вище, використаємо метод найменших квадратів, який
зводиться до аналізу частотної залежності квадратичного функціоналу
K
ˆ
F 2 1 R 2 nh , , (3.7)
2 K 1 n K
де