Page 97 - disertation_SLIEPKO_ROMAN

97

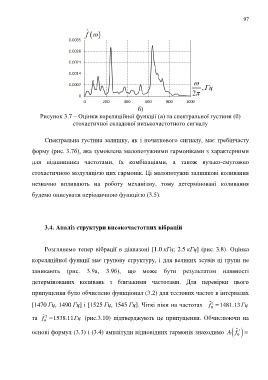
б)
Рисунок 3.7 – Оцінки кореляційної функції (а) та спектральної густини (б)
стохастичної складової низькочастотного сигналу

Спектральна густина залишку, як і початкового сигналу, має гребінчасту

форму (рис. 3.7б), яка зумовлена малопотужними гармоніками з характерними

для підшипника частотами, їх комбінаціями, а також вузько-смуговою

стохастичною модуляцією цих гармонік. Ці малопотужні залишкові коливання

незначно впливають на роботу механізму, тому детерміновані коливання

будемо описувати періодичною функцією (3.5).

3.4. Аналіз структури високочастотних вібрацій

Розглянемо тепер вібрації в діапазоні [1.0 кГц; 2.5 кГц] (рис. 3.8). Оцінка

кореляційної функції має групову структуру, і для великих зсувів ці групи не

заникають (рис. 3.9а, 3.9б), що може бути результатом наявності

детермінованих коливань з близькими частотами. Для перевірки цього

припущення було обчислено функціонал (3.2) для тестових частот в інтервалах

[1470 Гц, 1490 Гц] і [1525 Гц, 1545 Гц]. Чіткі піки на частотах f ˆ 0 1  14 81.13 Гц

та f ˆ 0 2  15 38.11 Гц (рис.3.10) підтверджують це припущення. Обчислюючи на

 
ˆ
1
основі формул (3.3) і (3.4) амплітуди відповідних гармонік знаходимо A f 0 