Page 185 - Microsoft Word - Дисертація.docx

185

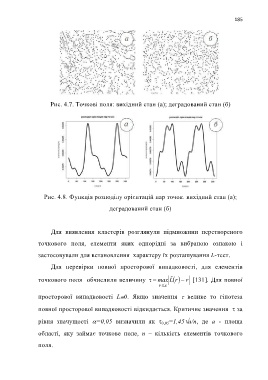
Рис. 4.7. Точкові поля: вихідний стан (а); деградований стан (б)

Рис. 4.8. Функція розподілу орієнтацій пар точок. вихідний стан (а);

деградований стан (б)

Для виявлення кластерів розглянули підмножини перетвореного

точкового поля, елементи яких однорідні за вибраною ознакою і

застосовували для встановлення характеру їх розташування L-тест.

Для перевірки повної просторової випадковості, для елементів

точкового поля обчислили величину =τ max L ( ) rr − [131]. Для повної
ˆ
r≤ s

просторової випадковості L≡0. Якщо значення τ велике то гіпотеза

повної просторової випадковості відкидається. Критичне значення τ за

рівня значущості α=0,05 визначили як τ 0,05 =1,45√a/n, де a - площа

області, яку займає точкове поле, n – кількість елементів точкового

поля.