Page 13 - Microsoft Word - автореферат_Косаревич.docx

11

операцією півтонового замикання для прямокутного вікна, величину якого
визначили з апріорної інформації про товщину тріщини. Після сканування
зображення поперек напрямку росту тріщини визначали координати елемента з
максимальною яскравістю рядка і приймали, що саме цей елемент відповідає
тріщині на зображенні. В результаті сегментації отримали бінарне зображення з
незв’язними сегментами тріщини. Застосувавши процедуру ітераційного з’єднання
сегментів зверху і знизу від максимального, отримали всю тріщину (Рис. 5г). Це
дало змогу визначати довжину тріщини в метричних одиницях виміру.
Отже, за величиною дисперсії яскравості елементів зображення стало
можливим не тільки локалізувати тріщину, але й ефективно усунути шуми у вигляді
яскравих бліків, що скорочує часу затрати на обробку зображення. В середньому це
дозволило зменшити абсолютну похибку вимірювання довжини тріщини у
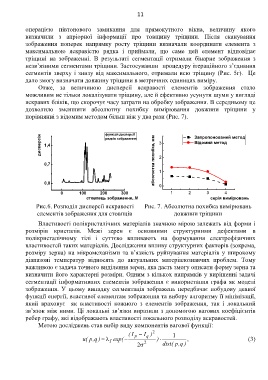
порівнянні з відомим методом більш ніж у два рази (Рис. 7).

функція дисперсії Запропонований метод
дисперсія 1,4 3 Відомий метод
рядків зображення

0,7 абсолютка похибка, мм 2
1

0,0 0

0 100 200 300 1 2 3 4
стовпець зображення, N серія вимірювань
Рис.6. Розподіл дисперсії яскравості Рис. 7. Абсолютна похибка вимірювань
елементів зображення для стовпців довжини тріщини

Властивості полікристалічних матеріалів значною мірою залежать від форми і
розмірів кристалів. Межі зерен є основними структурними дефектами в
полікристалічному тілі і суттєво впливають на формування електрофізичних
властивостей таких матеріалів. Дослідження впливу структурних факторів (зокрема,
розміру зерна) на мікромеханізми та в’язкість руйнування матеріалів у широкому
діапазоні температур відносять до актуальних матеріалознавчих проблем. Тому
важливою є задача точного виділення зерен, яка дасть змогу описати форму зерна та
визначити його характерні розміри. Одним з кількох напрямків у вирішенні задачі
сегментації інформативних елементів зображення є використання графа як моделі
зображення. У цьому випадку сегментація зображень передбачає побудову деякої
функції енергії, властивої елементам зображення та вибору алгоритму її мінімізації,
який враховує як властивості кожного з елементів зображення, так і локальний
зв’язок між ними. Ці локальні зв’язки виразили з допомогою вагових коефіцієнтів
ребер графу, які відображають властивості локального розподілу яскравостей.
Метою досліджень став вибір виду компонентів вагової функції:

I ( − I ) 2 1
( u q , p ) λ= I exp(− p q )⋅ , (3)
2σ 2 dist ( q , p )