Page 184 - КЛАСИФІКАЦІЯ ЛОКАЛІЗОВАНИХ ДЕФЕКТІВ ЗВАРНИХ ШВІВ НА РЕНТГЕНІВСЬКИХ ЗОБРАЖЕННЯХ ТРУБ

184

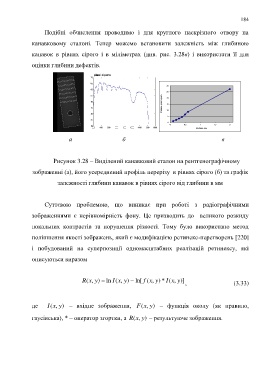
Подібні обчислення проводимо і для круглого наскрізного отвору на

канавковому еталоні. Тепер можемо встановити залежність між глибиною

канавок в рівнях сірого і в міліметрах (див. рис. 3.28в) і використати її для

оцінки глибини дефектів.

30
25
глибина, рівні сірого 20
15
10
5
0
0 0.5 1 1.5 2
глибина, мм
а б в

Рисунок 3.28 ‒ Виділений канавковий еталон на рентгенографічному

зображенні (а), його усереднений профіль перерізу в рівнях сірого (б) та графік

залежності глибини канавок в рівнях сірого від глибини в мм

Суттєвою проблемою, що виникає при роботі з радіографічними

зображеннями є нерівномірність фону. Це призводить до великого розкиду

локальних контрастів та порушення різкості. Тому було використано метод

поліпшення якості зображень, який є модифікацією ретинекс-перетворень [220]

і побудований на суперпозиції одномасштабних реалізацій ретинексу, які

описуються виразом

R (x , ) y  ln I (x , ) y  ln[ f (x , ) y * I (x , y )]
, (3.33)

де I (x , ) y – вхідне зображення, F (x , ) y – функція околу (як правило,

гаусівська), * – оператор згортки, а ( yxR , ) – результуюче зображення.